Question

I need help on a question

Answer 1

Law of Sines

Part A

Sine theorem

We are going to use in this problem the Law of Sines:

`(A)/(\sin(a))=(B)/(\sin (b))`

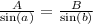
This is, in any triangle if we divide a side with its opposite angle sine,we will obtain the same result.

Sine theorem applied to this case

In this case:

the side h and the angle tº are opposite

and

the side y and the angle ∠LGM are opposite

then,

`(h)/(\sin(tº))=(y)/(\sin (\angle LGM))`

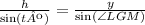
Finding the angle ∠LGM

Using the given information, we have that the angles sº and tº are complementary, this means that their together form a 90º angle:

sº + tº = 90º

then

sº = 90º - tº

Since the sum of all the inner angles of a triangle is 180º, and we have that ΔLGM is a right triangle, then

∠LGM + tº + 90º = 180º

then for ∠LGM, we have that

∠LGM = 180º - 90º - tº

∠LGM = 90º - tº

then ∠LGM and sº are the same angle: 90º - tº

∠LGM = sº

We can replace sº by ∠LGM in the equation we found:

`\begin{gathered} (h)/(\sin(tº))=(y)/(\sin(\angle LGM)) \\ \downarrow \\ (h)/(\sin(tº))=(y)/(\sin(sº)) \end{gathered}`

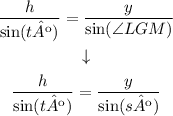
If we multiply both sides by sin(tº), we have:

`\begin{gathered} (h)/(\sin(tº))=(y)/(\sin(sº)) \\ \downarrow \\ h=(y)/(\sin(sº))\cdot\sin (tº) \end{gathered}`

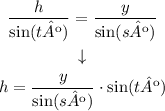
Answer A: h = y · sin(tº)/sin(sº)

Part B

We have that y = 3m, and sº = 38º

in order to find h using the equation we found, we must find tº. Since sº and tº are complementary,

sº + tº = 90º

then

tº = 52º

Now, we can replace in the equation:

`\begin{gathered} h=(y)/(\sin(sº))\cdot\sin (tº) \\ \downarrow \\ h=(3m)/(\sin (38º))\cdot\sin (52º) \end{gathered}`

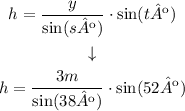
since

sin(52º) ≅ 0.79

and

sin (38º) ≅ 0.62

then

`\begin{gathered} h=(3m)/(0.62)\cdot0.79 \\ \downarrow \\ h=3m\cdot1.27=3.82m \end{gathered}`

Then, the height of the tree would be 3.82m

Answer B: 3.82 meters