Question

(0,7) (1,5) (1.5,3) (2,5) (2.3,3.2) ( 3,2) (3.5,4) the regression line is y= the correlation coefficient is r=

Answer 1

1) In this question, we can start setting our table:

2) Now let's find the regression line by finding the slope and the linear coefficient, according to these formulas below:

So

`\begin{gathered} m=(41.86-12.3*24.2)/(6*32.79-(32.79)^2) \\ m=0.2911\approx0.29 \\ b=(24.2-0.29*12.3)/(6) \\ b=3.4388\approx b=3.44\text{ } \end{gathered}`

Therefore we can write the regression line as:

`y=0.29x\text{ +3.44 }`

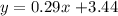
3) Now let's find the correlation coefficient through another formula:

`\begin{gathered} r=\frac{n\Sigma xy\text{ - (}\Sigma x)(\Sigma y)}{\sqrt[]{\lbrack n(\Sigma x)^2-(\Sigma x)^2\lbrack}n\Sigmay^2-\Sigmay^2)\text{ }} \\ r=\frac{6*41.86-12.3*24.2}{\sqrt[]{(6*(12.3)^2)(6*(24.2)^2-24.2)}} \\ r=-0.0261 \end{gathered}`