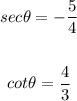Question

Let θ be an angle in quadrant III such that =sinθ−35. Find the exact values of secθ and cotθ.

Answer 1

Given:

Given θ is an angle in Quadrant III.

`\sin\theta=-(3)/(5)`

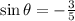
Required:

To find the value of secθ and cotθ.

Step-by-step explanation:

In Quadrant III, cosine (the x-value of the unit circle) and sine (the y-value of the unit circle) are both negative and tangent is positive.

`\begin{gathered} \sin\theta=-(3)/(5) \\ \\ =-(opp)/(adj) \end{gathered}`

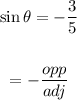
To find the adjacent side of the triangle use the Pythagorean Theorem:

`\begin{gathered} x^2+(-3)^2=5^2 \\ x^2=25-9 \\ x^2=16 \\ x=\pm4 \end{gathered}`

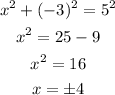
Since we are in the third quadrant

`x=-4`

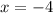
One way to find the secant and cotangent is to use the inverse identities:

`\begin{gathered} sec\theta=(1)/(\cos\theta) \\ \\ =(1)/(-(4)/(5)) \\ \\ =-(5)/(4) \end{gathered}`

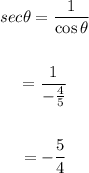
And

`\begin{gathered} cot\theta=(1)/(\tan\theta) \\ \\ =(1)/(-(3)/(-4)) \\ \\ =(4)/(3) \end{gathered}`

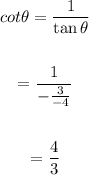
Final Answer:

`\begin{gathered} sec\theta=-(5)/(4) \\ \\ cot\theta=(4)/(3) \end{gathered}`