Question

Lamar invested his savings in two investment funds. The amount he invested in Fund A was $8000 less than the amount he invested in Fund B. Fund A returneda 2% profit and Fund B returned a 5% profit. How much did he invest in Fund B, if the total profit from the two funds together was $1030?

Answer 1

Lamar invested is savings in two funds

Let the investment in fund B be $x

The investment in fund A will be $(x - 8000)

Fund A returned 2% anf fund B returned 5% profit

ROI on fund A is 2% and ROI on fund B is 5%

Let the profit of fund A be a

Let the profit of fund B be b

The formula to find the return on investment (ROI) is

`\text{ROI}=\frac{\text{Profit }}{Investment}*100\text{\%}`

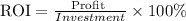
To find the profit for A, by substituting the

`\begin{gathered} \text{ROI}=2\text{\%} \\ \text{Investment}=x-8000 \\ \text{Profit=a} \end{gathered}`

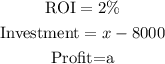
The profit of A is

`\begin{gathered} 2=(a)/(x-8000)*100 \\ \text{Crossmultiply} \\ 2(x-8000)=100a \\ \text{Divide both sides by 100} \\ a=(2(x-8000))/(100) \\ a=(x-8000)/(50) \\ a=0.02x-160 \end{gathered}`

To find the profit for B, by substituting the

`\begin{gathered} \text{ROI}=5\text{\%} \\ \text{Investment}=x \\ \text{Profit}=b \end{gathered}`

The profit of B is

`\begin{gathered} 5=(b)/(x)*100 \\ \text{Crossmultiply} \\ 5x=100b \\ \text{Divide both sides by 100} \\ (5x)/(100)=(100b)/(100) \\ b=0.05x \end{gathered}`

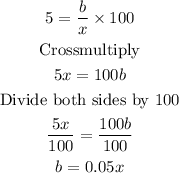
Sum of the total profit is

`\begin{gathered} \text{Profit of A + Profit of B =\$1030} \\ a+b=1030 \end{gathered}`

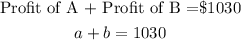
Substitute for a and b into the above expression

`\begin{gathered} (0.02x-160)+0.05x=1030 \\ 0.02x-160+0.05x=1030 \\ \text{Collect like terms} \\ 0.02x+0.05x=1030+160 \\ 0.07x=1190 \\ \text{Divide both sides by 0.07} \\ (0.07x)/(0.07)=(1190)/(0.07) \\ x=\text{\$17000} \end{gathered}`

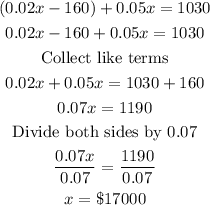
Hence, the investment in fund B, x, is $17,000