We are given that a radio isotope has an initial mass of 60 grams and a half-life of 11 years. The mass of the isotope with respect to time can be modeled using the following exponential function:

Where:
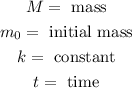
Now, since we are given that the half-life is 11 years this means that the mass will be half of the initial mass when "t = 11 years". We can use this fact to calculate the value of "k". Substituting half the initial mass we get:

Now, we may cancel the initial mass:
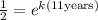
Now, we solve for "k". To do that we will take natural logarithm to both sides:
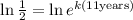
Now, we use the following property of logarithms:
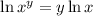
Applying the property we get:
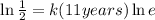
We have that:
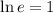
Therefore:
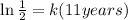
Now, we divide both sides by 11:

Solving the operations:
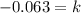
Now, we substitute in the formula for the mass:

Now, to determine the value of the mass after 25 years we substitute the value "t = 25", we get:
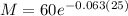
Solving the operations:
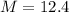
Therefore, the mass after 25 years is 12.4 grams.