Question

Which table identifies the x-values, if any, of the relative extrema of f(x) = (x^3 – 5x^2 + 11x – 11)e^x

Answer 1

Relative minimum: x=0

Relative maximum: None

Explanation:

Relative extrema are going to be located where the first derivative changes sign. Therefore, we must first find the derivative of the function:

`f'(x)=(d)/(dx)[(x^3-5x^2+11x-11)e^x]\\ \\f'(x)=(x^3-5x^2+11x-11)*(d)/(dx)(e^x)+[(d)/(dx)(x^3-5x^2+11x-11)]*e^x\\ \\f'(x)=(x^3-5x^2+11x-11)e^x+(3x^2-10x+11)e^x\\\\f'(x)=(x^3-2x^2+x)e^x\\\\f'(x)=xe^x(x^2-2x+1)\\\\f'(x)=xe^x(x-1)^2`

Next, we set
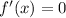`f'(x)=0` where we determine our critical points:

`0=xe^x(x-1)^2`

`x=0,x=1`

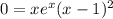
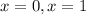
We then test points around the critical points to find where the derivative changes sign. I will use the points
`x=1`,
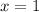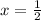`x=(1)/(2)`, and
`x=(3)/(2)`:

`f'(-1)=(-1)e^(-1)((-1)-1)^2=-(1)/(e)(-2)^2=-(4)/(e)<0\\\\f'((1)/(2))=(1)/(2)e^(1)/(2)((1)/(2)-2)^2=(√(e))/(2)(-(1)/(2))^2=(√(e))/(8)>0\\\\f'((3)/(2))=(3)/(2)e^(3)/(2)((3)/(2)-2)^2=(3√(e^3) )/(2)((1)/(2))^2=(3√(e^3))/(8)>0`

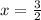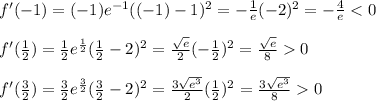
As you can see, the derivative changes sign from negative to positive at
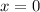`x=0`, but the sign stays positive at
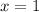`x=1`. Therefore, the only critical point that is an extreme point is
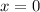`x=0`, which is a relative minimum. This means that there is no relative maximum.

In conclusion, the 4th option is correct. Review the graph for a visual of how the derivative sign changes.