We have two functions.
They can be linear or exponential.
We can evaluate the rate of change for each function.
If the rate of change is constant, we have a linear function.
For f(x) we can prove that when x increases by one unit, f(x) increases by 5.5 units, for any value of x.
Then, we can conclude that f(x) is a linear function.
If we look at g(x), we can see that the slope or rate of change is not constant, so it is not linear.
If g(x) is an exponential function, they have constant ratio: the quotient between consecutive values of g(x) is constant for all values of x:
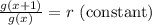
We can test this for the values of the table:
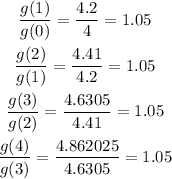
Then, we have proved that the ratio is constant and, therefore, g(x) is an exponential function.
We then can guess the function from:
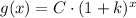
We can find C from g(0):
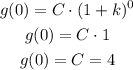
and k as:

the factor (1+k) is equal to the ratio we have just calculated (1.05).
Then, the function can be written as:
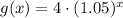
Answer:
f(x) is linear, while g(x) is exponential.
The formula for g(x) is 4*1.05^x