The nth term of a geomeric series having first term 'a' and the common ratio 'r' is given by,
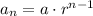
Now, consider the given geometric sequence,
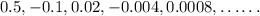
Observe that the first term of the sequence is 0.5,
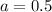
The common difference is calculated as,
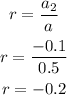
Substitute the values,
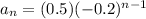
This expression is given in option C. Therefore, option C is the correct choice.