Question

Convert the following system of equations into an augmented matrix: (1) 2x + 2y + 2z = 4(2) -x − 3y = 2 + 8z − 3y(3) -z = 2x + y

Answer 1

ANSWER and EXPLANATION

We want to transform the system of equations given into an augmented matrix.

First, we have to put the equations in the form:

`\begin{gathered} a_1x+b_1y+c_1z=k^{} \\ a_2x+b_2y+c_2z=l \\ a_3x+b_3y+c_3z=m \end{gathered}`

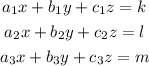
where k, l, and m are constants

a1, a2, a3, b1, b2, b3, c1, c2, and c3 are coefficients of x, y, and z in the equations

Therefore, we have that the equations become:

`\begin{gathered} \Rightarrow2x+2y+2z=4 \\ -x-3y+3y-8z=2 \\ \Rightarrow-x-8z=2 \\ \Rightarrow2x+y+z=0 \end{gathered}`

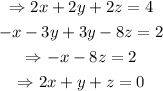
The augmented matrix will be in the form:

From the above equations, we have that the coefficients and constants are:

`\begin{gathered} a_1=2;b_1=2;c_1=2;k=4 \\ a_2=-1;b_2=0;c_2=-8;l=2 \\ a_3=2;b_3=1;c_3=1;m=0 \end{gathered}`

Therefore, the augmented matrix is: