Question

How much work is required to accelerate a proton from rest up to a speed of 0.995 c?

Answer 1

The amount of work required to accelerate a proton from rest up to a speed of 0.995c, is 1.35×10⁻⁹ J

How to calculate the work required?

The Lorentz factor is paramount in calculating the work required. Thus, we shall obtain the Lorentz factor. Details below:

• Speed of proton (v) = 0.995c
• Lorentz factor (γ) = ?

`\gamma = \frac{1}{\sqrt{1\ -\ (v^2)/(c^2)}}\\ \\\gamma = \frac{1}{\sqrt{1\ -\ ((0.995c)^2)/(c^2)}} \\\\\gamma = (1)/(√(1\ -\ 0.995^2))}\\\\\gamma = 10`

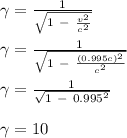
Now, we shall calculate the work required to accelerate the proton. Details below:

• Lorentz factor (γ) = 10
• Speed of light (c) = 3×10⁸ m/s
• Mass of proton (m) = 1.67×10⁻²⁷ Kg
• Work required (W) =?

W = (γ - 1)mc²

= (10 - 1) × 1.67×10⁻²⁷ × (3×10⁸)²

= 1.35×10⁻⁹ J

Thus, the work required is 1.35×10⁻⁹ J