Question

At what angles should a 60kg painter place his ladder against the wall?

Answer 1

We will have the following:

First, we find all the forces in x & y, that is:

`\sum ^{}_{}F_x=0\Rightarrow\sum ^{}_{}F_x=F_f-N_1\colon N_1=F_f`

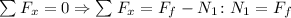
Here Ff is the frictional force and N1 the normal force on the point where the ladder is resting.

`\sum ^{}_{}F_y=0\Rightarrow\sum ^{}_{}F_y=N_2-mg-Mg\colon N_2=(M+m)g`

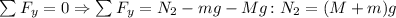
Here N2 is the normal force of the resting point of the ladder on the ground. M is the mass of the person and m is the mass of the ladder.

Then we make sure that the ladder won't rotate, that is the momentum will be 0, that is:

`\sum ^{}_{}\tau_i=mg\cos (\theta)(l/3)+mg\cos (\theta)(l/2)-N_2\cos (\theta)l+F_f\sin (\theta)l=0`

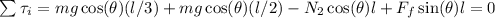
Here "l/3" represents the positons of the person to climb, and "l/2" represents the position of the center of mass of the ladder.

Then, we remember that we are given the static friction coefficient, and replace:

`\sum ^{}_{}\tau_i=mg\cos (\theta)(l/3)+mg\cos (\theta)(l/2)-(M+m)g\cos (\theta)l+\mu_s(M+m)g\sin (\theta)l=0`

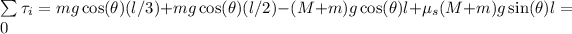
Then we divide the whole expression by cos(theta) in order to eliminate all extra trigonometric values and determie the angle:

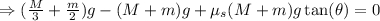
`\Rightarrow((M)/(3)+(m)/(2))g-(M+m)g+\mu_s(M+m)g\tan (\theta)=0`
`\Rightarrow((M)/(3)+(m)/(2))-(M+m)+\mu_s(M+m)\tan (\theta)=0`

`\Rightarrow\theta=\tan ^(-1)((45)/(35))\Rightarrow\theta=\tan ^(-1)((9)/(7))`
`=\theta=52.12501635\ldots\Rightarrow\theta\approx52.1`

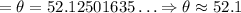
So, the angle would be approximately 52.1°.

***Screenshot***