Question

The quadratic x^2 + (3/2)x - 1 has the following unexpected property: the roots, which are 1/2 and -2, are one less than the final two coefficients. Now find a quadratic with a leading term x^2 such that the final two coefficients are both non-zero, and the roots are one more than these coefficients.

a) x^2 + 4x + 9
b) x^2 - 3x + 2
c) x^2 + 3x - 2
d) x^2 - 4x - 9

Answer 1

b)
`x^2 - 3x + 2 because The quadratic x^2 - 3x + 2` has roots 3 ± 1, making them one more than the final two coefficients, fulfilling the specified condition.

Step-by-step explanation:

The given quadratic
`x^2 + (3/2)x - 1`has roots 1/2 and -2, and the roots are one less than the final two coefficients. To find a quadratic with roots one more than the coefficients, we look for a quadratic of the form
`x^2 + bx + c where the roots are (b + 1) and (c + 1).`

Comparing this with the options provided:

`a) x^2 + 4x + 9 (roots: -4 ± √(-4) = complex roots)b) x^2 - 3x + 2 (roots: 3 ± 1)c) x^2 + 3x - 2 (roots: -3 ± √13 = complex roots)d) x^2 - 4x - 9 (roots: 4 ± √40 = complex roots)`

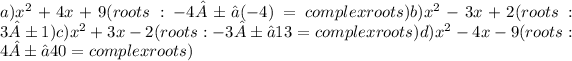
Option b)
`x^2 - 3x + 2` fits the criteria with roots 3 ± 1, and these roots are indeed one more than the final two coefficients. Therefore, option b) is the correct quadratic that satisfies the given conditions.