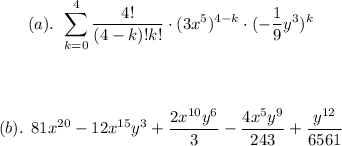1 Answer

Ask a Question

Matt Sugden · Answer 1 · 2023-04-06T11:30:30+0000

Given the expression:

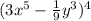
Given that Harold uses boinomial theorem to expand the given binomial, let's solve for the following:

• (a). What is the sum in summation notation that he uses the express the expnansion.

Apply the formula:

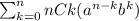
$\sum ^n_(k=0)nCk(a^(n-k)b^k)$

Therefore, the sum in summation nottation will be:

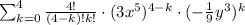
$\sum ^4_(k=0)(4!)/((4-k)!k!)\cdot(3x^5)^(4-k)\cdot(-(1)/(9)y^3)^k$

• (b). Write the simplified terms of the expansion.

To write the simplified terms, we have:

$\begin{gathered} (4!)/(4-0)!0!)*(3x^5)^(4-0)\cdot(-(1)/(9)y^3)^0+(4!)/((4-1)!1!)\cdot(3x^5)^(4-1)\cdot(-(1)/(9)y^3)^1+(4!)/((4-2)!2!)\cdot(3x^5)^(4-2)\cdot(-(1)/(9)y^3)^2+(4!)/((4-3)!3!)\cdot(3x^5)^(4-3)\cdot(-(1)/(9)y^3)^3+(4!)/((4-4)!4!)\cdot(3x^5)^(4-4)\cdot(-(1)/(9)y^3)^4 \\ \\ \\ 81x^(20)-12x^(15)y^3+(2x^(10)y^6)/(3)-(4x^5y^9)/(243)+(y^(12))/(6561) \end{gathered}$

ANSWER:

$\begin{gathered} (a)\text{. }\sum ^4_(k=0)(4!)/((4-k)!k!)\cdot(3x^5)^(4-k)\cdot(-(1)/(9)y^3)^k \\ \\ \\ (b)\text{. }81x^(20)-12x^(15)y^3+(2x^(10)y^6)/(3)-(4x^5y^9)/(243)+(y^(12))/(6561) \end{gathered}$

0 Comments

Your comment on this question:

Your answer

1 Answer

0 Comments

Your comment on this answer:

Other Questions