Question

The tables below represents a system of two linear equations in two variables, What is the solution to the system of equations?

Answer 1

Answer:

x = 3, y = 4

Explanations:

Let us find the equations represented by each of the tables

Calculate the slope for table 1 selecting the points (2, 5) and (3, 4)

`\begin{gathered} m\text{ = }(y_2-y_1)/(x_2-x_1) \\ m\text{ = }(4-5)/(3-2) \\ \text{m = }(-1)/(1) \\ m\text{ = -1} \end{gathered}`

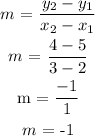
The equation of the line is given as:

`\begin{gathered} y-y_1=m(x-_{}x_1) \\ y\text{ - 5 = -1(x - 2)} \\ y\text{ - 5 = -x + 2} \\ y\text{ = -x + 2 + 5} \\ y\text{ = -x + 7} \end{gathered}`

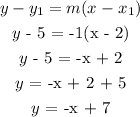
The equation represented by the first table is y = -x + 7

Calculate the slope for table 2 by selecting the points (0, 1) and (1, 2)

`\begin{gathered} m\text{ = }(2-1)/(1-0) \\ m\text{ = 1} \end{gathered}`
`\begin{gathered} y-y_1=m(x-x_1) \\ y\text{ - 1 = 1 (x - 0)} \\ y\text{ - 1 = x} \\ y\text{ = x + 1} \end{gathered}`

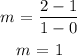
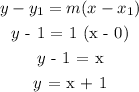
The equation represented by the second table is y = x + 1

The system of equations is:

y = -x + 7..........(1)

y = x + 1...........(2)

Equating equations (1) and (2)

-x + 7 = x + 1

x + x = 7 - 1

2x = 6

x = 6/2

x = 3

Substitute the value of x into equation (2)

y = 3 + 1

y = 4

The solution to the system of equations is x = 3, y = 4