Question

How do I multiply, subtract, add, and divide fractions?

Answer 1

Step 1: How to multiply Fractions

Fractions are number that have two-part numerator and denominator e.g

`(3)/(4),\frac{5}{4\text{ }}`

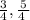
To multiply fractions, you multiply the numerator and denominator

Examples:

`(5)/(7)*(3)/(4)=(5*3)/(7*4)=(15)/(28)`

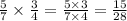
Then you reduce the result to the lowest form if possible.

Step 2: How to Divide fractions

Dividing a fraction is very similar to the multiplication of fractions. Just that you are to change the division symbol to multiplication and then you take the reciprocal of the fraction.

Example:

5/8 ÷ 3/4

This will become

`(5)/(8)*(4)/(3)=(5)/(2)*(1)/(3)=(5)/(6)`

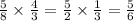
Note that the 4 at the numerator is used to divide 8 at the denominator

Step; How to Add and Subtract Fractions

To add or subtract fraction, you make use of the LCM of the denominators

Examples:

`\begin{gathered} (5)/(8)+(4)/(5) \\ \text{The denominators are 8 and 5 whose LCM is 40} \\ (5)/(8)+(4)/(5) \\ =(25+32)/(40)=(57)/(40)=1(17)/(40) \end{gathered}`

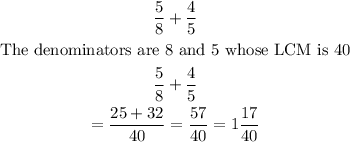
Note that: Divide the denominator by the LCM and multiply the result by the numerator

Similarly for subtraction

`\begin{gathered} (5)/(6)-(3)/(4) \\ \text{The LCM of the denominators is 24} \\ (5)/(6)-(3)/(4) \\ =(20-18)/(24)=(2)/(24)=(1)/(12) \end{gathered}`

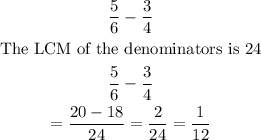
Note that you can also use a similar approach to Mixed Fractions

For mixed fractions, you can convert the fraction to an improper fraction and follow the approach above.

Alternatively, you can use this

Example

`\begin{gathered} 4(3)/(5)-2(1)/(3) \\ \text{The mixed fraction has two part, the whole number and proper fraction} \\ 4(3)/(5)-2(1)/(3)=(4-2)((3)/(5)-(1)/(3)) \end{gathered}`
`\begin{gathered} \text{Then we have} \\ 2((9-5)/(15))=2(4)/(15) \end{gathered}`

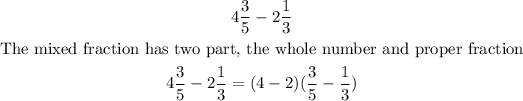
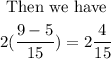
A similar method also goes for addition.