Question

The escape speed from the surface of Planet Zoroaster is 24.0 km/s. The planet has no atmosphere. A meteor far away from the planet moves at speed 2.00 km/s on a collision course with Zoroaster. How fast is the meteor going when it hits the surface of the planet? km/s

Answer 1

We are asked to determine the velocity of a meteor when it hits a planet. To do that we need to use conservation of energy.

`K_0+K_e=K_f`

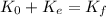
Where:

`\begin{gathered} K_0=\text{ initial kinetic energy} \\ K_e=\text{ kinetic energy gained when entering the planer} \\ K_f=\text{ final kinetic energy} \end{gathered}`

The meteor has initial kinetic energy, then when it enters the planet it gains kinetic energy due to the gravitational field of the planet. When we add these together we get the final kinetic energy.

The kinetic energy is determined using the following formula:

`K=(1)/(2)mv^2`

And, the kinetic energy due to the gravitational field is determined using the escaped velocity. Therefore, we substitute in the energy balance and we get:

`(1)/(2)mv^2_0+(1)/(2)mv^2_e=(1)/(2)mv^2_f`

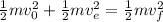
Where:

`\begin{gathered} m=\text{ mass of the meteor, }\lbrack m\rbrack \\ v_0,v_f=\text{ initial and final velocities,}\lbrack(m)/(s)\rbrack \end{gathered}`

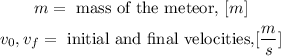
Now, we can cancel out the mass and the 1/2:

`v^2_0+v^2_e=v^2_f`

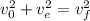
Now we solve for the final velocity by taking the square root to both sides:

`\sqrt[]{v^2_0+v^2_e}=v_f`

Now, we substitute the values:

Solving the operations:

Therefore, the final velocity of the meteor is 24.08 km/s.