Question

Solve the following for the equation:•Symmetric with respect to ___So the function is even or odd?•X and y intercepts•Period beginning and ending0 ≤ ( __ ) ≤ 2π•10 points on the graph.(2 periods)•Label graph with x and y values.

Answer 1

We have the function:

`y=-(5)/(2)+\cos \lbrack3(x-(\pi)/(6))\rbrack`

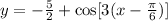
a) We have to find if this function has any symmetry.

As this function can be considered a linear transformation of the cosine function and the argument is also a linear transformation of x, this function may have the same symmetries of the cosine function.

The cosine function is an odd function, as it is symmetric around the origin. It satisfy the following expression:

`\begin{gathered} f(x)=-f(-x) \\ \cos (x)=-\cos (-x) \end{gathered}`

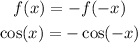
But in this case, as y is translated 5/2 units down, so this condition does not apply anymore.

Then, this function is neither even nor odd.

It is periodic around y = -5/2 but it is not symmetric.

b) It has nox-intercepts, as the maximum value of the function is -3/2.

The y-intercept happens when x = 0 and can be calculated as:

`\begin{gathered} y=-(5)/(2)+\cos (3(0-(\pi)/(6)) \\ y=-(5)/(2)+\cos (-(\pi)/(2)) \\ y=-(5)/(2)+0 \\ y=-(5)/(2) \end{gathered}`

c) To calculate the period, we take into account that the period of a periodic function is the difference of the values of x that have the same y-value and derivative.

In this case, we can compare the value for this points:

`\begin{gathered} \cos (0)=\cos (2\pi) \\ x_1\Rightarrow3(x_1-(\pi)/(6))=0\Rightarrow x_1=(\pi)/(6) \\ x_2\Rightarrow3(x_2-(\pi)/(6))=2\pi \\ x_2-(\pi)/(6)=(2)/(3)\pi \\ x_2=((2)/(3)+(1)/(6))\pi \\ x_2=(5\pi)/(6) \end{gathered}`

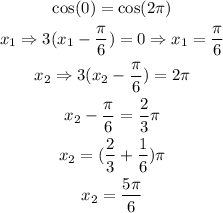
Then, the function will have completed a cycle between x = π/6 and x = 5π/6.

The period will be the difference between those two values:

`T=x_2-x_1=(5\pi)/(6)-(\pi)/(6)=(4\pi)/(6)=(2\pi)/(3)`

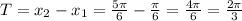
NOTE: we could have estimated the period from the argument of the cosine. We have a frequency of 3 multiplying the variable (-π/6 is the phase), so we can divide the cycle 2π by 3 and get 2π/3 as period.

The period is 2π/3.

d) We can use the extreme values of the cosine function and relate them to x and y.

We can complete the table:

Then, graping the points we can sketch the function as:

To graph the function, we can divide the x values in intervals of π/6.

We start with x = 0, for which y = -5/2.

Then we increase x by π/6 and y will increase to -3/2, its maximum value.

Then, we increase x by π/6 again (to π/3) and y will decrease to the mean value of -5/2.

If we increase x by π/6 again (to 3π/6 = π/2), y will decrease to its minimum value of -7/2.

Finally, if we increase x by π/6 (to 4π/6 = 2π/3), y will increase to the mean value of -5/2 and we have now completed a cycle.

We can increase x by π/6 and this cycle will be repeated.

NOTE: from the graph we can see that the function can be considered symmetric around the point (0,-5/2).

Answer:

The function is symmetric around the point (0,-5/2).

The function is neither even nor odd.

There are no x-intercepts and the y-intercept is at y = -5/2.

The period is T = 2π/3.