Question

Watch help videoIan is working two summer jobs, making $19 per hour lifeguarding and making $9per hour clearing tables. In a given week, he can work no more than 14 total hoursand must earn a minimum of $180. If e represents the number of hours lifeguardingand y represents the number of hours clearing tables, write and solve a system ofinequalities graphically and determine one possible solutionInequality 1: y zInequality 2; y 2

Answer 1

Given:

Amount he earns lifeguarding = $19 per hour

Amount he earns clearing table = $9 per hour

Maximum amount of hours he can work in a week = 14 hours.

This is expressed as: e + y ≤ 14

Minimum amount he must earn = $180.

This is expressed as: 19e + 9y ≥ 180

Let e represent the number of hours lifeguarding

Let y represent the number hours clearing tables.

We have the system of inequaties:

19e + 9y ≥ 180......................inequality 1

e + y ≤ 14................................inequality 2

Let's solve for y using substitution method.

Subtract y from both sides in inequality 1:

e + y - y ≤ 14 - y

e ≤ 14 - y

Substitute (14 - y) for e in inequality 1:

19(14 - y) + 9y ≥ 180

266 - 19y + 9y ≥ 180

266 - 10y ≥ 180

Subtract 266 from both sides:

266 - 266 - 10y ≥ 180 - 266

-10y ≥ -86

Divide both sides by -10:

`(-10y)/(-10)\ge(-86)/(-10)`

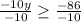
Solving further:

`y\le8.6`

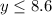
Therefore, the number of hours Ian must use in clearing the tables should be no more than 8.6 hours

To solve for e, substitute 8.6 for y in either of the inequalities.

Substitute 8.6 for y in inequality 2:

The graph of the inequalities is below:

e + y ≤ 14

e + 8.6