Question

-3(x-14)+9x=6x+42what does that equal? is it true or false

Answer 1

We are given the following equation

`-3\mleft(x-14\mright)+9x=6x+42`

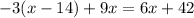
Let us solve the equation for x.

Step 1:

Multiply the term -3 with the terms in the parenthesis.

`\begin{gathered} -3(x-14)+9x=6x+42 \\ -3x+42+9x=6x+42 \end{gathered}`

Step 2:

Simplify the terms on the left-hand side of the equation

`\begin{gathered} -3x+42+9x=6x+42 \\ 42+6x=6x+42 \end{gathered}`

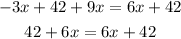
Step 3:

Combine the like terms together.

`\begin{gathered} 42+6x=6x+42 \\ 42-42=6x-6x \\ 0=0 \end{gathered}`

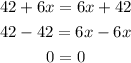
This means that this equation has an infinite number of possible solutions.

If you notice the left and right side of the equation are exactly the same.

`42+6x=6x+42`

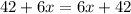
This means that whatever value of x you put into this equation, the equation will always be satisfied.

Try substituting some values for x.

`\begin{gathered} 42+6(1)=6(1)+42 \\ 42+6=6+42 \\ 48=48 \end{gathered}`
`\begin{gathered} 42+6(-2)=6(-2)+42 \\ 42-12=-12+42 \\ 30=30 \end{gathered}`

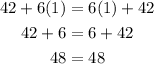
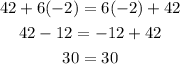
Hence, the given equation has an infinite number of possible solutions.