Question

I have a Statistics question. I lost my tutor.Assume you had a random sample of 50 graduate students' GRE scores, and you calculated a mean score of 300 with a standard deviation of 47. Using a confidence level of 95%, calculate and interpret every aspect of the confidence level. Margin of error:Upper Bound:Lower Bound:Interpretation (hint: if we were to randomly sample from this population 100 times, what is the probability the sample mean GRE scores will fall between the upper and lower bounds?)

Answer 1

The confidence interval for the population mean has the following structure:

`\lbrack\bar{x}\pm Z_{1-(\alpha)/(2)}\cdot\frac{\sigma}{\sqrt[]{n}}\rbrack`

You have to add/subtract the margin of error to the point estimation.

The point estimation of the population mean is the sample mean, in this case, the sample mean is 300.

The margin of error is the second term of the formula:

`Z_{1-(\alpha)/(2)}\cdot\frac{\sigma}{\sqrt[]{n}}`

-First, you have to determine the z-value to use for the confidence interval. To do so you have to use the confidence level:

`1-\alpha=0.95`

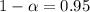
Determine the value of 1-α/2

`\begin{gathered} \alpha=1-0.95 \\ \alpha=0.05 \\ (\alpha)/(2)=0.025 \\ 1-(\alpha)/(2)=1-0.025=0.975 \end{gathered}`

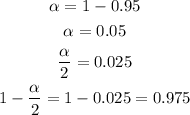
You have to use the Z-value that accumulates 0.975 of probability, that is:

`Z_(0.975)=1.96`

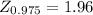
Next, calculate the margin of error:

`\begin{gathered} Z_{1-(\alpha)/(2)}\frac{\sigma}{\sqrt[]{n}} \\ 1.96\cdot\frac{47}{\sqrt[]{50}}=13.0277 \end{gathered}`

The margin of error rounded to the nearest hundredth is 13.03.

Subtract the margin of error from the mean to determine the lower bound:

`\begin{gathered} \bar{x}-Z_{1-(a)/(2)}\cdot\frac{\sigma}{\sqrt[]{n}} \\ 300-13.03=286.97 \end{gathered}`

Add the margin of error to determine the upper bound:

`\begin{gathered} \bar{x}+Z_{1-(\alpha)/(2)}\cdot\frac{\sigma}{\sqrt[]{n}} \\ 300+13.03=313.03 \end{gathered}`

The 95% confidence interval is [286.97;313.03]

The confidence level of a confidence interval indicates the probability that the confidence interval will contain the true value of the estimated parameter. So if you were to construct 100 intervals, you would expect 95 of them to include the population parameter.

In terms of the exercise, you can interpret the calculated interval, with a 95% confidence level, you expect the interval [286.97;313.03] to contain the true value of the average GRE scores.