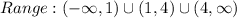Question

I need help I think we also need to graph it too if you can help with that

Answer 1

The function is;

`r(x)=(x^2-4)/(x^2-3x+2)`

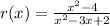
Factorizing the numerator and the denominator, we have;

`r(x)=((x-2)(x+2))/((x-1)(x-2))`

There is a hole at x = 2.

Cancelling the common x - 2 terms, we have;

`r(x)=(x+2)/(x-1)`

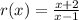
The hole exists at the point ( 2, 4 );

`r(2)=4`

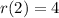
The y-intercept is the point (0, -2 ) ;

The x-intercept is at the point ( -2. 0) ; Since

`\begin{gathered} x+2=0 \\ x=-2 \end{gathered}`

The horizontal asymptote is the line;

`y=1`

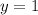
The vertical asymptote is the line;

`x=1`

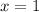
The graph is plotted below;

Clearly, all attributes of the graph is evident here.

The domain and range of the function is;

`Domain:(-\infty,1)\cup(1,2)\cup(2,\infty)`

The range is;

`Range:(-\infty,1)\cup(1,4)\cup(4,\infty)`