Question

Supposed that the demand d. for candy at a theater is inversely related to the price p. (A) when the price if candy is $3.25 per bag, the theater sells 144 bags of candy. Express the demand for candy in terms of its price. (B) determine the number of candy that will be sold if the price is raised to $4.00 a bag. (A). Write the equation that relates D to p. (B) the theater will sell how many bags of candy if the price is raised to $4.00 a bag

Answer 1

From the question given, we are told that the demand D for bags, is inversely related to the price p. This is mathematically written as

`\begin{gathered} D\propto(1)/(p) \\ \propto is\text{ a sign of proportionality. } \end{gathered}`

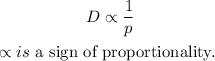
If the proportionality sign is removed, a constant k will be introduced, and this becomes

`D=(k)/(p)`

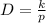
(A) We are told that when the price per bag is $3.25, demand is 144 bags.

Hence D = 144 and p = 3.25, now let's find k using the equation above

`\begin{gathered} D=(k)/(p) \\ 144=(k)/(3.25) \\ k=144*3.25 \\ k=468 \end{gathered}`

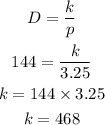
Hence the equation that relates D to p is

`D=(468)/(p)`

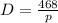
(B) If the price is raised to $4.00 per bag, the theater will sell?

Using the relationship, this becomes

`\begin{gathered} D=(468)/(p) \\ D=(468)/(4.00) \\ D=117\text{ bags } \end{gathered}`

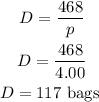
Hence the answer is 117 bags.