Solution:
Given:
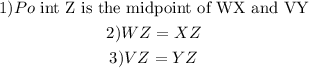
To complete the proof,
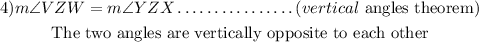
The figure can now be split into two triangles as shown below;
From the image drawn above showing corresponding parts of both triangles, we can deduce that,
![\begin{gathered} 5)\Delta VZW\cong\Delta YZX\ldots\ldots\ldots..(side-angle-side\text{ congruency theorem)} \\ \\ \text{The two triangles are congruent by SAS having 2 corresponding equal sides and 1 corresponding equal angle.} \end{gathered}]()
Since the two triangles have been proven to be congruent, then
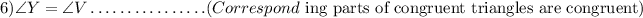
Therefore,

Thus, the correct table that correctly completes the students proof is;