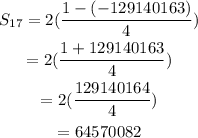The formula for the sum of a geometric series is given as:
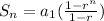
Note that r is the common ratio, a1 is the first term.
To find the common ratio, find the ratio of any two consecutive terms, say a1 and a2:
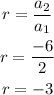
Next, substitute the values n=17, r=-3, and a1=2 into the formula:
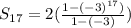
Use a calculator to evaluate the expression for the sum: