Question

Diane starts to get frustrated that the plane is off-course, so she takes the controls. Shewants to get the plane to fly at an angle of 25° North of East, with a resultantgroundspeed of 140 kilometers per hour. She knows she must "aim" the airplane at anangle that compensates for wind. At what angle should she direct the airplane to fly?

Answer 1

We know that the wind is blowing from north to south with a speed of 32 km per hour, let's call the wind vector W, then it can be written as

`\vec{W}=-32\hat{j}`

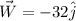
We also know that Diane wants the plane to fly north of east at an angle of 25° and a speed of 140 km/h. This means that the resultant should be

`\vec{R}=140\cos 24\hat{i}+140\sin 24\hat{j}`

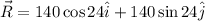
Now, we would like to know at what angle Diane should fly tha plane. To find this we will introduce a vector T whose magnitud and direction are unknown.

Then

`\vec{T}=T\cos \theta\hat{i}+T\sin \hat{j}`

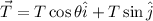
Now, we know that the resultant is

`\vec{R}=\vec{T}+\vec{W}`

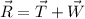
then

`\begin{gathered} 140\cos 25\hat{i}+140\sin 25\hat{j}=T\cos \theta\hat{i}+T\sin \theta\hat{j}+(-32\hat{j}) \\ 140\cos 25\hat{i}+140\sin 25\hat{j}=T\cos \theta\hat{i}+(T\sin \theta-32)\hat{j} \end{gathered}`

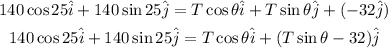
Since the unit vector i and j are independent this gives us two equations

`\begin{gathered} 140\cos 25=T\cos \theta \\ 140\sin 25=T\sin \theta-32 \end{gathered}`

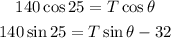
From the first equation we have that

`T=(140\cos 25)/(\cos \theta)`

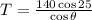
Plugging the value of T in the second equation we have

`140\sin 25=((140\cos25)/(\cos\theta))\sin \theta-32`

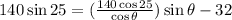
Now we need to solve this equation for theta.

`\begin{gathered} 140\sin 25=((140\cos25)/(\cos\theta))\sin \theta-32 \\ 140\sin 25+32=(140\cos 25)(\sin \theta)/(\cos \theta) \\ (\sin\theta)/(\cos\theta)=(140\sin 25+32)/(140\cos 25) \end{gathered}`

Now we have to remember that

`(\sin\theta)/(\cos\theta)=\tan \theta`

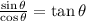
hence

`\begin{gathered} \tan \theta=(145\sin 25+32)/(145\cos 25) \\ \theta=\tan ^(-1)((145\sin 25+32)/(145\cos 25)) \\ \theta=35.7 \end{gathered}`

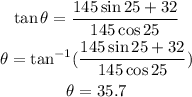
Therefore Diane has to direct the airplane at an angle of 35.7° North of east.