Question

Calculus ! please help and if u cannot reject me quick many have

Answer 1

Answer: The behavior of the function can be checked by finding the derivative of it and evaluating it at the two specified points:

`\begin{gathered} f(x)=|x^2-9| \\ \\ \\ (df(x))/(dx)=(|x^2-9|)/(x^2-9)(2x) \end{gathered}`

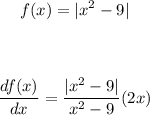
The behaviour at x = -3 and x = 3.

`\begin{gathered} (df(x))/(dx)=(\lvert x^(2)-9\rvert)/(x^(2)-9)(2x) \\ \\ \\ x=3\rightarrow(\lvert3^2-9\rvert)/(3^2-9)(2*3)=(0)/(0)*6=0\rightarrow\text{ Not possible} \\ \\ x=-3\rightarrow(\lvert(-3)^2-9\rvert)/((-3)^2-9)(2*-3)=(0)/(0)(-6)\rightarrow\text{ Not possible} \\ \end{gathered}`

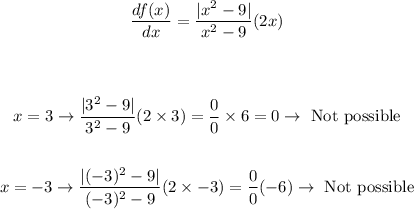
The answer therefore is:

`\text{ Option\lparen D\rparen}\rightarrow\text{ Continuous but non-Differentiable }`

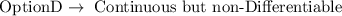
Plot for the function:

Not that the f(x) is indeed Differentiable function

, but there can not be any slope at x = -3 and x = 3.