Question

The principal P is borrowed, and the loan’s future value A, at time t is given. Determine the loan’s simple interest rate r to the nearest tenth of a percent.A= $2840P= $2300t= 9 months

Answer 1

Step 1. Gather all of the information.

We have the Principal P:

`P=2300`

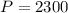
The total amount A for the loan's future value:

`A=2840`

And the time t in moths:

`t=9\text{months}`

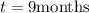
We are going to need the time in years, so we consider that 9 months are 9/12 of a year:

`t=(9)/(12)\text{years}`

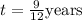
Which can be simplified to 3/4 of a year:

`t=(3)/(4)`

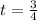
Step 2. Remember the simple interest formula:

`A=P(1+rt)`

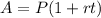
From this formula, we will need to find the simple interest rate r, so we will solve for r.

-The first step to solve for r is to divide both sides by P:

`(A)/(P)=(P)/(P)(1+rt)`

on the right-hand side P/P is 1 so we are left only with 1+rt:

`(A)/(P)=1+rt`

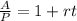
-the second step to solve for r is to subtract 1 to both sides:

`(A)/(P)-1=1-1+rt`

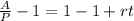
On the right-hand side, 1-1 cancels each other:

`(A)/(P)-1=rt`

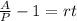
-the last step to solve for r is to divide both sides by t:

`((A)/(P)-1)/(t)=r`

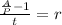
This is the equation we will use to find the value of r.

Step 3. Substitute the known values into the formula to find r:

`\begin{gathered} r=((A)/(P)-1)/(t) \\ r=((2840)/(2300)-1)/((3)/(4)) \end{gathered}`

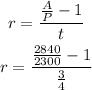
We have substituted the values of A, P and t.

Simplifying the fractions:

`r=(1.2348-1)/(0.75)`

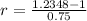
Solving the final operations:

`\begin{gathered} r=(0.2348)/(0.75) \\ r=0.313 \end{gathered}`

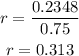
This is the simple interest rate represented in decimal form, to convert it to percentage, we need to multiply the result by 100:

`\begin{gathered} r=0.313*100 \\ r=31.3 \end{gathered}`

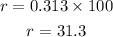
The final result is 31.3%

Answer:

the simple interest rate to the nearest tenth is:

31.3%