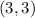Question

This is one part to the question, the next five parts of the question will be revealed upon answering the previous part correctly Part one: the domain is?

Answer 1

Given:

The parabola equation is,

`f\mleft(x\mright)=-3\mleft(x-3\mright)^2+3`

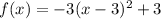
To find:

domain and range of the graph.

Step-by-step explanation:

Domain:

The domain of a function is the set of input values for which the function is real and defined.

the function here dose not have any undefined points. So,

the domain is,

with the vertex,

`(x_v,\: y_v)`
`\begin{gathered} if\: a<0\: \text{ the range is,}f\mleft(x\mright)\le\: y_v \\ \text{if }\: a>0\text{ the range is, }f\mleft(x\mright)\ge\: y_v \end{gathered}`

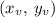
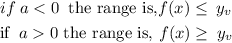
then,

`\begin{gathered} a=-3 \\ \text{vertices: (}x_v,\: y_v)=(3,\: 3) \end{gathered}`

hence,

`f\mleft(x\mright)\le\: 3`

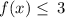
The maximum point is (3,3).

Final Answer:

Domain of the parabola is,

`-\infty\: <strong>Range of the parabola is,</strong>[tex]f\mleft(x\mright)\le\: 3`

in interval notation the range is,

`\: \: (-\infty\: ,\: 3\rbrack`

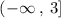
the vertex of the parabola is,

`(3,3)`