Question

Write a system of equations to describe the situation below, solve using elimination, and fill in the blanks.Helen and Jordan decided to shoot arrows at a simple target with a large outer ring and a smaller bull's-eye. Helen went first and landed 3 arrows in the outer ring and 1 arrow in the bull's-eye, for a total of 174 points. Jordan went second and got 3 arrows in the outer ring and 4 arrows in the bull's-eye, earning a total of 444 points. How many points is each region of the target worth?

Answer 1

Steps1: Define a parameter for the unknow

`\begin{gathered} a=\text{outer ring point } \\ b=\text{bull's eye point} \end{gathered}`

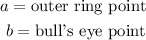
Step2: Write out the equation for Helen

Since Helen landed 3arrows on the outer ring and 1 on the bull's eye and have a total of 174, the equation becomes

`3a+b=174`

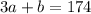
Step3: Wite out the equation for Jordan

Since Jordan Landed 3arrows on outer ring and 4arrows in the bull's eye with a total point of 444, the equation becomes

`3a+4b=444`

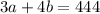
Step4: Solve the system of equation with elimination method

To solve the equation, we label them eliminate the variables separately

hence

`\begin{gathered} 3a+b=174\ldots Eq1 \\ 3a+4b=444\ldots Eq2 \end{gathered}`

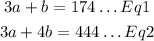
Subtract Eq1 from Eq2 (Eq2-Eq1) to eliminate the variable a.

`\begin{gathered} 3a_{}+4b=444 \\ 3a+b=174 \\ \text{Then} \\ 3b=270 \end{gathered}`

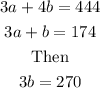
From the equation in the last line above divide both sides by 3, we have

`\begin{gathered} (3b)/(3)=(270)/(3) \\ \text{then} \\ b=90 \end{gathered}`

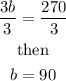
To eliminate the variable b, Multiply Eq1 by 4 and subtract from Eq 2, we have

`\begin{gathered} 4* Eq1\rightarrow4(3a+b=174)=12a+4b=696 \\ \text{Then subtract from Eq2, we have } \\ 12a+4b=696 \\ 3a+4b=444 \\ \text{hence} \\ 9a=252 \end{gathered}`

From the equation in the last line above, divide both sides by 9, we obtain

`\begin{gathered} (9a)/(9)=(252)/(9) \\ \text{Then} \\ a=28 \end{gathered}`

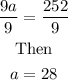
Hence

a=28,b=90.

Therefore

The outer ring worth 28 point

The bull's eye worth 90 point