Question

There are 15 players on a soccer team. Only 11 players can be on the field for a game. How many different groups of players of 11 players can the coach make, if the position does not matter?

Answer 1

1,365

Explanation:

I got it right on the test.

Answer 2

Given:

There are 15 players on a soccer team.

Only 11 players can be on the field for a game.

We will find the number of groups of players of 11 players can the coach make.

Note: the position does not matter, so, we will use the combinations

We will use the following formula:

`^nC_r=(n!)/((n-r)!*r!)`

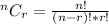
substitute n = 15, and r = 11

`^(15)C_(11)=(15!)/((15-11)!*11!)=(15*14*13*12*11!)/(4*3*2*1*11!)=(32760)/(24)=1365`

So, the answer will be:

The number of different groups = 1365