Question

Identify the transformations of the function ƒ(x) = log22(x + 6) from the base graph g(x) = log2(x).There are two transformations: 1. a vertical stretch of the curve by a factor of 2 and 2. a shift to the right of 12 units.There are two transformations: 1. a horizontal compression of the curve by a factor of 2 and 2. a shift to the left of 12 units.There are two transformations: 1. a vertical compression of the curve by a factor of 2 and 2. a shift to the left of 12 units.There are two transformations: 1. a horizontal stretch of the curve by a factor of 2 and 2. a shift to the right of 12 units.

Answer 1

B. There are two transformations: 1. a horizontal compression of the curve by a factor of 2 and 2. a shift to the left of 12 units.

Explanation:

We have the following function:

`\begin{gathered} f(x)=\log_22(x+6)\rightarrow\log_2(2x+12) \\ \\ g(x)=\log_2(x) \end{gathered}`

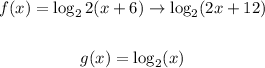
We have to add or subtract within the logarithm it represents a horizontal shift, in the case of adding the added amount moves to the left and if it is subtracted it moves that amount to the right. In this case it adds 12, which means that it moves to the left by 12 units.

When multiplying inside the function, by a value k, there is a horizontal change, in a factor k. If this value is greater than one it would be horizontal compression but if the value is between 0 and 1 it would be horizontal stretch.

In this case, it is multiplied by 2, which is greater than 1, which means that there is a horizontal compression of factor 2.

Which means that the correct answer is B. There are two transformations: 1. a horizontal compression of the curve by a factor of 2 and 2. a shift to the left of 12 units.