Question

Listed below are foot lengths (mm) and heights (mm) of males. Find the regression equation, letting foot length be the predictor (x) var best predicted height of a male with a foot length of 273.3 mm. How does the result compare to the actual height of 1776 mm?Foot Length 282.4 278.0 253.2 259.0 278.7 258.1 274.2 262.0Height 1784.6 1771.0 1675.6 1646.2 1859.2 1710.2 1789.3 1737.3

Answer 1

A. The coefficient of determination is 0.743. 74.3% of the variation is explained by the linear correlation and 25.7% is explained by other factors.

Explanation:

The coefficient of determination is the percentage variation in y explained by all the x variables together.

It is the square of the correlation coefficient.

Using a regression calculator:

Thus:

`\begin{gathered} \text{ The coefficient of determination}=r^2 \\ =0.8516^2 \\ =0.7252 \end{gathered}`

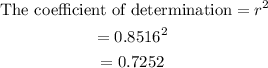
The closest result from the options is 0.743.

Therefore, the coefficient of determination is 0.743. 74.3% of the variation is explained by the linear correlation and 25.7% is explained by other factors.

Option A is correct.