Question

Identify the holes, vertical and horizontal asymptotes of each. Then sketch a graph #6

Answer 1

- We are given the following function:

`(-2x-2)/(x+3)`

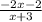
- We are asked to find the holes, vertical, and horizontal asymptotes, and to plot them.

- The question can be solved if we know the rules on how to derive holes, vertical and horizontal asymptotes from functions.

Holes:

- Holes are derived when we can have a common factor (x - a) in the numerator and denominator. The hole, in this case, is x = a.

Horizontal Asymptote:

Given that n is the highest degree of the numerator and m is the highest degree of the denominator, and an is the coefficient of the highest degree of the numerator and bm is the coefficient of the highest degree of the denominator, we have that:

1. If n2. If n=m, then y=an / bm is the horizontal asymptote. That is, the ratio of the leading coefficients.

3. If n>m, there is no horizontal asymptote. However, if n=m+1, there is an oblique or slant asymptote.

Vertical Asymptote:

- This is gotten by equating the denominator to zero. The value of x from doing this gives the value of the vertical asymptote.

- With the above explanation, we can proceed to solve the question

.

Checking for a Hole:

- There is no common factor shared between the numerator and denominator, thus, there is no hole.

Checking for Horizontal Asymptote:

- The ratio of the leading coefficients for the highest degree of the numerator and denominator is given by:

`\begin{gathered} -(2)/(1)=-2 \\ \\ \therefore y=-2\text{ is a Horizontal Asymptote} \end{gathered}`

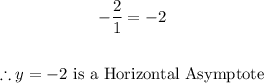
Checking for Vertical Asymptote:

Equating the denominator to zero, we have:

`\begin{gathered} x+3=0 \\ \text{Subtract 3 from both sides} \\ x=-3 \end{gathered}`

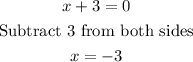
Thus, we have that:

Horizontal Asymptote: y = -2

Vertical Asymptote: x = -3

- Plotting the graph of the function and its asymptotes, we have: