The arc length can be calculated by using the following formula
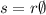
theta, is the central angle of the arc in radians, and r is the radius
We have been given that the radius is 18, and the central angle is 150 degrees. To find the arc length, let us start by converting the angle to radians. We can do this by multiplying 150 by the ratio between radians and degrees (pi/180). This works because 180 degrees is equal to pi radians (so the fraction is equal to 1):
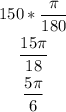
So, the sector is 5pi/6 radians. Now, we can solve this by multiplying this by the radius of the circle:
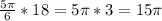
Therefore, the answer is C, or 15pi