Question

Please help me figure out what and how to do it

Answer 1

In order to find the polynomials that have these roots, we can use the factored form of a polynomial with 4 roots:

`P(x)=a(x-x_1)(x-x_2)(x-x_3)(x-x_4)_{}_{}`

So the polynomials that have the roots -1, -2, 3 and 7 are:

`P(x)=a(x+1)(x+2)(x-3)(x-7)`

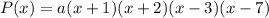
Since a can be any real value, so there is an infinite number of polynomials with these roots.

If the polynomial has 4 roots, it is a 4th-degree polynomial.

Since (x-7) is a factor of P(x), we can write P(x) = (x-7)Q(x).

The degree of Q(x) is 3, since one of the roots was "removed" from P(x).

Since (x+8) is not a factor of P(x), we can't write P(x) = (x+8)Q(x).