Step 1:
Concept: Use the two theorems below to find the measure of angle QRS
1. The sum of angles in a triangle is 180 degrees
2. The sum of angles on a straight line is 180 degrees.
Step 2:
Angle QRP is on a straight line with angle QRS = 20x + 12
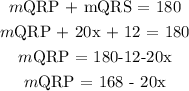
Step 3:
Sum of angles in a triangle = 180
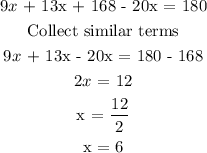
Final answer
m
= 20(6) + 12
= 120 + 12
= 132 Option C