So,
We could use the formula of an ideal gas:
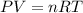
Where P is the pressure of the gas in atm, V is the volume in L, R is a constant, n represents the number of moles of the gas, and T is the temperature in K.
Given that we know that:
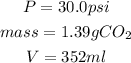
We should convert some units first to use the equation.
The pressure units have to be expressed in atm!
1psi = 0.068atm, so:
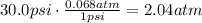
The volume units have to be expressed in Liters!
1L = 1000ml, so:
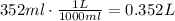
Now, remember that we need to find the number of moles of the gas (n). We could use the fact that the number of moles of a compound is equal to:
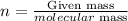
In this case, our given mass is 1.39g CO2.
The molecular mass of a compound can be found if we multiply the number of atoms of each element by their molar mass, and then sum all these results. This is,
Therefore, the number of moles contained in 1.39g of CO2 are:
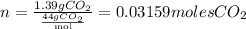
Now that we have P = 2.04, V = 0.352, n = 0.03159 and R = 0.082, we could replace all these values in the equation given. Remember that R is a given value which is 0.082.
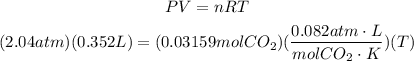
To find T, we solve the last equation for T:
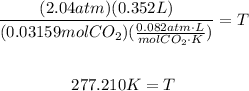
Therefore, the temperature inside the can was 277.210°K.
We need this result in °C, so we substract 273.15:
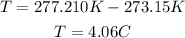
Finally, the temperature of the pop was 4.06°C. So, it was cold.