This is a graph of the three initial points. Now we are going to graph the midpoints A and B.
But, first let's calculate the midpoints.
To calculate the average points we will use the following formula

For A
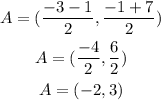
For B
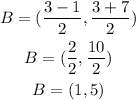
The graph shows the midpoints and the originals.
Visually we can check that the lines of those points are parallel. However, we are going to calculate the slopes of the points to prove it.
To calculate the slopes we will use the following formula
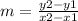
Slope AB

Slope PR

As the slopes are equal we can conclude that the two segments are parallel.
Finally, we will calculate the length of each of the segments.
To calculate the length of the segments we will use the following formula
![d=\sqrt[]{(x2-x1)^2+(y2-y1)^2}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/r4sbek1l8stpiydtifcm.png)
For AB
![\begin{gathered} d_(AB)=\sqrt[]{(1-(-2)^2+(5-3)^2} \\ d_(AB)=\sqrt[]{3^2+2^2} \\ d_(AB)=\sqrt[]{9+4} \\ d_(AB)=\sqrt[]{13} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ze9ijndetaankz0ssjh0.png)
For PR
![\begin{gathered} d_(PR)=\sqrt[]{(3-(-1))^2+(3-(-3))^2} \\ d_(PR)=\sqrt[]{4^2+6^2} \\ d_(PR)=\sqrt[]{16+36} \\ d_(PR)=\sqrt[]{52} \\ d_(PR)=2\sqrt[]{13} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/gjcsbhtmpfulcvi65dbt.png)
Now we can see that the PR segment is twice the AB segment