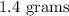Question

The half life of a substance is 12 days. If there are 4.5 grams to start with, how much will be left after 20 days? Round to the nearest tenth of a gram. Be sure to label your answer.

Answer 1

The amount of a decaying substance with half life τ that remains after a time t, if the initial amount of that substance is A_0, is given by the formula:

`A(t)=A_0\cdot2^{-(t)/(\tau)^{}}`

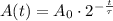
If the half life of that substance is 12 days, and the initial amount of that substance is 4.5 grams, then A_0=4.5 and τ=12. Substitute those values as well as t=20 to find the remaining amount after 20 days:

`\begin{gathered} A(t)=4.5*2^{-(t)/(12)} \\ \Rightarrow A(20)=4.5*2^{-(20)/(12)} \\ =4.5*2^{-(5)/(3)} \\ =4.5*0.3149\ldots \\ =1.4174\ldots \end{gathered}`

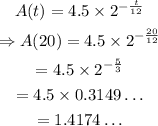
To the nearest tenth of a gram, the remaining amount after 20 days, is:

`1.4\text{ grams}`