1) Solving the system of equations:
y=2x²+6-10 ⇒ y =2x² -4
y=-x+5 x (-1)
1.2 Rewriting it and Subtracting
y =2x²- 4
-y =+x-5
----------------------
0=2x²+x -9
2) Now solving that quadratic equation 2x²+x -9=0, using the Resolutive formula:
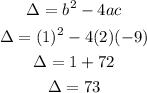
![\begin{gathered} x=\frac{-b\pm\sqrt[]{\Delta}}{2a} \\ x=\frac{-1\pm\sqrt[]{73}}{4} \\ x_1=\frac{-1-\sqrt[]{73}}{4} \\ x_2=\frac{-1+\sqrt[]{73}}{4} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/fgm8pepywh9kfamrhiz3.png)
3) Now plugging in back into the II equation y=-x+5
![\begin{gathered} y=-(\frac{-1-\sqrt[]{73}}{4})+5 \\ y=\frac{1+\sqrt[]{73}}{4}+5 \\ y=\frac{21+\sqrt[]{73}}{4} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/o37gm7fetwqqpvx10n0b.png)
3.1Plugging the x solutions into y=2x²-4
![\begin{gathered} y=2(\frac{-1-\sqrt[]{73}}{4})^2-4 \\ y=\frac{21+\sqrt[]{73}}{4} \\ y=2(\frac{-1+\sqrt[]{73}}{4})^2-4\text{ =}\frac{21-\sqrt[]{73}}{4} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/p2zrgjusvk9jx3keltvr.png)
After checking in both of the original equations, there is only one valid x solution.
So the solution to that system is
![x=\frac{-1-\sqrt[]{73}}{4}\text{ and }y=\frac{21+\sqrt[]{73}}{4}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/dg2m4wpfo5ihg1ud5qew.png)