Question

The school that Ashley goes to is selling tickets to a fall musical. On the first day of ticket sales the school sold 9 adult tickets and 3 student tickets for a total of $120. The school took in $22 on the second day by selling 1 adult ticket and 1 student ticket. What is the price each of one adult ticket and one student ticket?

Answer 1

Given:

On first day, the number of adult tickets sold, p=9.

On first day, the number of student tickets sold, q=3.

The total price of tickets sold on first day, t=$120.

On second day, the number of adult tickets sold, m=1.

On second day, the number of student tickets sold, n=1.

The total price of tickets sold on second day, T=$22.

Let x be the price of one adult ticket and y be the price of one student ticket.

Hence, the expression for the total price of tickets sold on first day is,

`\begin{gathered} t=px+qy \\ 120=9x+3y\text{ ---(1)} \end{gathered}`

The expression for the total price of tickets sold on second day is,

`\begin{gathered} T=mx+ny \\ 22=x+y\text{ ---}(2) \end{gathered}`

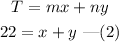
Now, multiply equation (2) by 3.

`\begin{gathered} 3*22=3x+3y \\ 66=3x+3y\text{ ---(3)} \end{gathered}`

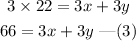
Subtract equation (3) from equation (1) and solve for x.

`\begin{gathered} 120-66=9x+3y-3x-3y \\ 54=6x \\ x=(54)/(6) \\ x=9 \end{gathered}`

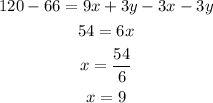
So, x=9.

Now, substitute x=9 in equation (2) and solve for y.

`\begin{gathered} 22=9+y \\ y=22-9 \\ y=13 \end{gathered}`

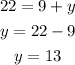
Therefore, the price of each adult ticket is $9 and the price of each student ticket is $13.