Question

Prove ABCD is a square A(2,4) B(4,-1) C(-1,-3) D(-3,2)

Answer 1

First, let's check if all segments have the same length, calculating the distance between the points using the formula:

`d=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2}`

So we have:

`\begin{gathered} AB\colon \\ d=\sqrt[]{(-1-4)^2+(4-2)^2}=\sqrt[]{25+4}=\sqrt[]{29} \\ \\ BC\colon \\ d=\sqrt[]{(-3-(-1))^2+(-1-4)^2}=\sqrt[]{4+25}=\sqrt[]{29} \\ \\ CD\colon \\ d=\sqrt[]{(2-(-3))^2+(-3-(-1))^2_{}_{}}=\sqrt[]{25+4}=\sqrt[]{29} \\ \\ AD\colon \\ d=\sqrt[]{(4-2)^2+(-3-2)^2}=\sqrt[]{4+25_{}}=\sqrt[]{29} \end{gathered}`

Now, we need to check the slopes of each segment. The adjacent sides need to be perpendicular, so their slopes need to have the relation:

`m_2=-(1)/(m_1)`

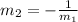
Calculating the slopes with the formula below, we have:

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ \\ AB\colon \\ m=(-1-4)/(4-2)=-(5)/(2) \\ \\ BC\colon \\ m=\frac{-3-(-1)_{}}{-1-4}=(2)/(5) \\ \\ CD\colon \\ m=(2-(-3))/(-3-(-1))=-(5)/(2) \\ \\ AD\colon \\ m=(4-2)/(2-(-3))=(2)/(5) \end{gathered}`

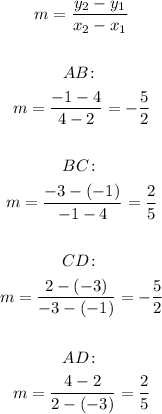
So all adjacent sides are perpendicular.

All sides have the same length and all adjacent sides are perpendicular, therefore ABCD is a square.