Question

Find rectangular coordinates for each point with the given polar coordinates

Answer 1

Step-by-step explanation

Given the following points

A = (3, pi/4)

The standard from of a rectangular coordinate is given as

`(r,\text{ }\theta)`

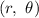
Where r = 3 and theta = pi/4

Step 1: convert radians to degrees

1 pi = 180 degrees

Therefore, pi/4 is

= 180/4

= 45 degrees

Step 2 : find cos 45 and sin 45

`\begin{gathered} \text{ Since, }\theta\text{ = 45} \\ \text{Then, cos 45 = }\frac{\sqrt[]{2}}{2}\text{ and sin 45}\frac{\sqrt[]{2}}{2} \end{gathered}`

Step 3: find the x and y - coordinates

x - coordinate = r x cos 45

y - coordinate = r x sin 45

`\begin{gathered} x\text{ - coordinate } \\ \text{r = 45 and cos 45 = }\frac{\sqrt[]{2}}{2} \\ \text{x - coordinate = }\frac{3\text{ x }\sqrt[]{2}}{2} \\ x\text{- coordinate = }\frac{3\sqrt[]{2}}{2} \\ \text{y - coordinate = r x sin 45} \\ \text{y - coordinate = 3 x }\frac{\sqrt[]{2}}{2} \\ \text{y - coordiante =}\frac{3\sqrt[]{2}}{2} \end{gathered}`

Therefore, the rectangular coordinate is

`(\frac{3\sqrt[]{2}}{2}\text{ , }\frac{3\sqrt[]{2}}{2})`