Given the identity:
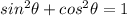
Let's find the value of tanθ, where:

Since it is in the given interval, θ is in the third quadrant.
Now, substitute -0.27 for θ in the identity:
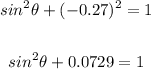
Subtract 0.0729 from both sides:
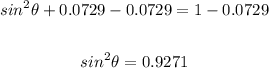
Take the square root of both sides:
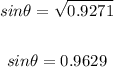
Now, apply the trigonometric identity:
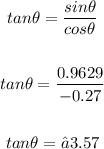
Since tan is positive in the third quadrant, we have:
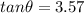
ANSWER:
3.57