Question

Dylan has a square peice of metal that measures 10inches on each side he cuts the metal along the diagonal, forming two right trianhles what is the the length of the hypotenuse of each right triangle to the nearest tenth of an inch

Answer 1

As per given by the question,

There are given that a sides and length of the four triangle.

Now,

Check one-by-one, whether triangles are right triangle or not.

Then,

For check the triangle is right triangle or not, use pythagoras theorem.

Now,

For first triangle,

The side is given,

Suppose ,

`A=12,\text{ B=24, and C=}\sqrt[]{439}`

Then,

From the pythagoras theorem,

`A^2+B^2=C^2`

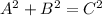
Put the value of A, B, and C in above formula;

So,

`\begin{gathered} 12^2+24^2=(\sqrt[]{439})^2 \\ 144+576=439 \\ 720\\e439 \end{gathered}`

Hence, first triangle is not a right angle triangle.

Now,

For second triangle,

`A=14,\text{ B=18, and C=}\sqrt[\square]{520}`

Then,

`\begin{gathered} A^2+B^2=C^2 \\ 14^2+18^2=(\sqrt[]{520})^2 \\ 196+324=520 \\ 520=520 \end{gathered}`

Hence, the second triangle is right angle triangle.

Now,

For third triangle,

`\begin{gathered} A^2+B^2=C^2 \\ 16^2+18^2=(\sqrt[]{421})^2 \\ 256+324=421 \\ 580\\e421 \end{gathered}`

Hence, the third triangle is not a right angle triangle.

Now,

For fourth triangle,

`\begin{gathered} A^2+B^2=C^2 \\ 15^2+18^2=(\sqrt[]{549})^2 \\ 225+324=549 \\ 549=549 \end{gathered}`

Hence, the fourth triangle is also a right triangle.

So,

The second and fourth triangle is right angle triangle.