You give to each number a letter:
Number 1: x
Number 2: y
The sum of two numbers is 2490:
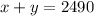
8.5% of x is equal to 6.5% of y:
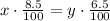
You use the equations above to find the numbers by substitution method:
1. Solve one of the variables in the first equation:
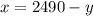
2. Substitute the variable x in the second equation by the value in step 1:
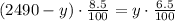
3. Solve the equation in step 2 and find the value of y:
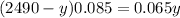
Remove parenthesis multipliying 0.085 for both terms in the parenthesis:
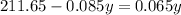
Add 0.085y in both sides of the equation:
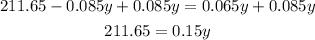
Divide into 0.15 both sides of the equation:
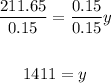
4. Use the value of y to find x:
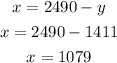
Then, the numbers are x=1079 and y=1411