Question

Bob, a farmer in Florida, has an orange grove. In the grove are 120 trees. Each tree ordinarilyproduces 650 oranges. Bob would like to increase his orange production and knows that becauseof lost space and sunlight, each additional tree he plants will cause a reduction of 5 oranges fromevery tree.How many trees can Bob have in his grove in order to maximize his orange production? What isthe maximum number of oranges that Bob will produce with these trees?

Answer 1

Bob has 120 trees in the grove. Each tree produces about 650 oranges.

Bob wants to maximize this orange production by adding new trees to the grove. Space limitations and sunlight make it to reduce each tree's production by 5 oranges per tree added.

The total number of oranges actually produced is the product of the number of trees by the number of oranges per tree, that is, 120 * 650 = 78,000 oranges.

Now suppose Bob adds x trees to the grove. The new number of trees is 120 + x and each tree now produces 650 - 5x oranges.

The number of oranges produced under this new condition is:

`N=(120+x)\cdot\mleft(650-5x\mright)`

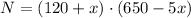
Operating:

`N=120\cdot650-600x+650x-5x^2`

Simplifying:

`N=78,000+50x-5x^2`

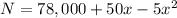
To maximize the number of oranges, we use derivatives:

`N^(\prime)=50-10x`

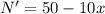
Equating the first derivative to 0:

`50-10x=0`

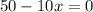
Solving for x:

x = 50 / 10 = 5

This means that Bob should add only 5 more orange trees to maximize production.

The new number of trees would be 120+5= 125 trees

Each tree would produce 650 - 5*5 = 625 oranges

The total production would be 125*625 = 78,125 oranges