Question

5. The distance between two buildings is 67 m. From the top of the shorter building, the angle of elevation to the top of the taller building is 27°. From the same position, the angle of depression to the base of the taller building is 39º. Calculate the height of the two buildings.

Answer 1

First, let's draw a scheme representing the measures in the text. Let's call the shorter building as A and the taller building as B.

Using this scheme, we can see that we have 2 right triangles. The height of the taller building(let's call it hB), is given by the following relation

`\frac{h_B_{}}{67}=\tan 39^o`

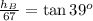
Then, calculating the height we have

`\begin{gathered} h_B=67\tan 39^o=67*0.80978403319\ldots=54.2555302241 \\ h_B\approx54.3 \end{gathered}`

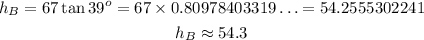
The difference between the height of the smaller building(let's call it hA) and the taller building, is given by

`((h_B-h_A))/(67)=\tan 27^o`

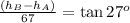
Solving for h_A, we have

`\begin{gathered} ((h_B-h_A))/(67)=\tan 27^o \\ (h_B-h_A)=67\tan 27^o \\ h_A=h_B-67\tan 27^o \\ h_A\approx20.1 \end{gathered}`

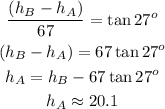
The height of the smaller building is 20.1m and the height of the taller building is 54.3m.