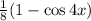Question

Use a power-reducing identity to rewrite the following expression below in terms containing only firstpowers of cosine.cos4(x)tan?(x)

Answer 1

Given:

`\cos ^4x\tan ^2x`

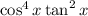
To rewrite: The expression below in terms containing only the first powers of cosine.

Step-by-step explanation:

Using the identity,

`\tan ^2x=(\sin ^2x)/(\cos ^2x)`

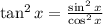
We can write,

`\begin{gathered} \cos ^4x\tan ^2x=\cos ^4x\cdot(\sin ^2x)/(\cos ^2x) \\ =\cos ^2x\cdot\sin ^2x \end{gathered}`

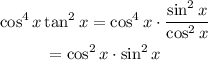
Using the identity,

`\sin ^2x=1-\cos ^2x`

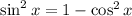
So, we can write,

`\begin{gathered} =\cos ^2x(1-\cos ^2x) \\ =\cos ^2x-\cos ^4x \\ =\cos ^2x-(\cos ^2x)^2 \end{gathered}`

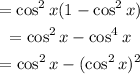
Using the identity,

`\cos ^2x=(1+\cos2x)/(2)`

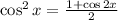
Substituting we get,

`\begin{gathered} =(1+\cos2x)/(2)-((1+\cos2x)/(2))^2 \\ =(1+\cos2x)/(2)-((1+\cos ^22x+2\cos 2x)/(4)) \\ =(1+\cos2x)/(2)-((1+\cos^22x+2\cos2x)/(4)) \\ =(1)/(2)+(\cos2x)/(2)-(1)/(4)-(\cos^22x)/(4)-(\cos 2x)/(2) \\ =(1)/(4)-(\cos^22x)/(4) \\ =(1)/(4)-((1+\cos4x)/(2))/(4) \\ =(1)/(4)-(1+\cos 4x)/(8) \\ =(1)/(4)-(1)/(8)-(\cos 4x)/(8) \\ =(1)/(8)-(\cos4x)/(8) \\ =(1)/(8)(1-cos4x) \end{gathered}`

Final answer: The power reduced form in terms of only first powers of cosine is,

`(1)/(8)(1-\cos 4x)`