Question

Find the final amount in the following retirement account, in which the rate of return on the account and the regular contribution change over time,$387 per month invested at 4%, compounded monthly, for 5 years; then $558 per month invested at 7%, compounded monthly, for 5 years.What is the amount in the account after 10 years?(Do not round until the final answer. Then round to the nearest dollar as needed.)

Answer 1

Answer:

The amount in the account after 10 years is approximately $65,607

Step-by-step explanation:

For the first 5 years, we have:

Principal = $387

Rate = 0.04/12

n = 5 * 12 = 60

Amount in the first 5 years is:

`\begin{gathered} (387((1+(0.04)/(12))^(60)-1))/((0.04)/(12)) \\ \\ =25657.706\ldots \end{gathered}`

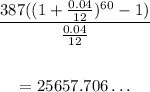
Amount after 5 years is:

P = $558

R = 0.07/12

n = 5 * 12 = 60

Amount is:

`\begin{gathered} (558((1+(0.07)/(12))^(60)-1))/((0.07)/(12)) \\ \\ =39948.839\ldots \end{gathered}`

Amount after 10 years is now:

`\begin{gathered} 25657.706\ldots+39948.839\ldots \\ =65606.544 \end{gathered}`

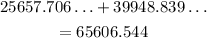
The amount is approximately $65,607